ISO 7626 pdf download

ISO 7626 pdf download Mechanical vibration and shock — Experimental determination of mechanical mobility — Part 1: Basic terms and definitions, and transducer specifications
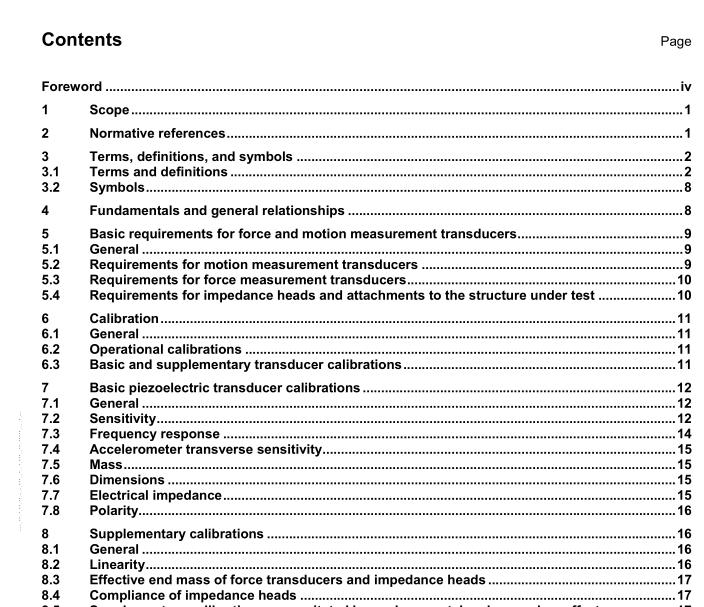
3 Terms, definitions, and symbols
3.1 Terms and definitions
For the purpose of this document, the terms and definitions given in ISO 2041 and the following apply.
NOTE As this part of ISO 7626 deals with mechanical mobility, the notes to the definitions below provide more detail than is given in ISO 2041.
3.1.1
frequency-response function
frequency-dependent ratio of the motion-response Fourier transform to the Fourier transform of the excitation force of a linear system
NOTE 1 Excitation can be harmonic, random or transient functions of time. The frequency-response function does not depend on the type of excitation function if the tested structure can be considered as a linear system in a certain range of the excitation or response. In such a case, the test results obtained with one type of excitation can be used for estimating the response of the system to any other type of excitation. Phasors and their equivalents for random and transient excitation are discussed in Annex B.
NOTE 2 Linearity of the system is a condition which, in practice, is met only approximately, depending on the type of system and on the magnitude of the input. Care has to be taken to avoid non-linear effects, particularly when applying impulse excitation. Structures which are known to be non-linear (e.g. certain riveted structures) should not be tested with impulse excitation and great care is required when using random excitation for testing such structures.
NOTE 3 Motion may be expressed in terms of velocity, acceleration or displacement; the corresponding frequency- response function designations are mobility (sometimes called mechanical admittance), accelerance (sometimes unfortunately called inertance; this term should be avoided because it is in conflict with the common definition of acoustic inertance and also contrary to the implication carried by the term inertance) and dynamic compliance (sometimes called receptance), respectively. These are summarized in Table 1. Each of these frequency-response functions is the phasor of the motion response at a point on a structure due to a unit force (or moment) excitation. The magnitude and the phase of these functions are frequecy dependent. Typical magnitude graphs for accelerance and for dynamic compliance, corresponding to the mobility graph shown in Figure 1, are shown in Figures 2 and 3, respectively.
NOTE 4 Frequency response functions can be further differentiated as
a) driving point response function, where the excitation and response are measured at the same location for the evaluation of the frequency-response function, e.g. the use of an impedance head for the measurements (i j in the formulae in Table 1);
b) transfer response function, where the excitation and response are not measured at the same location for the evaluation of the frequency-response function (i  j in the formulae in Table 1).
NOTE 5 Adapted from ISO 2041:2009, 1.53.