BS ISO IEC 15946-5 pdf download

BS ISO IEC 15946-5 pdf download Information technology — Security techniques — Crytographic technique based on elliptic curves Part 5: Elliptic curve generation
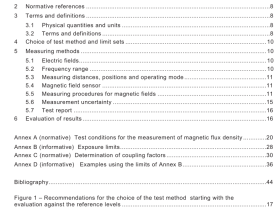
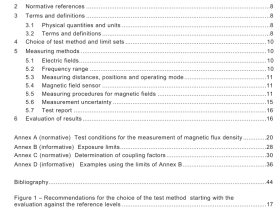
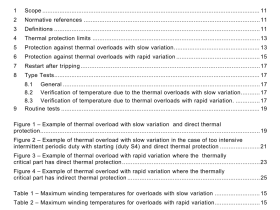
1 Scope
ISO/IEC 1 5946 specifies public-key cryptographic techniques based on elliptic curves. This part of ISO/IEC 1 5946 defines elliptic curve generation techniques useful for implementing the elliptic curve based mechanisms defined in ISO/IEC 9796-3, ISO/IEC 1 1 770-3, ISO/IEC 1 4888-3 and ISO/IEC 1 8033-2.
The scope of this part of ISO/IEC 1 5946 is restricted to cryptographic techniques based on elliptic curves defined over finite fields of prime power order (including the special cases of prime order and characteristic two). The representation of elements of the underlying finite field (i.e. which basis is used) is outside the scope of this part of ISO/IEC 1 5946. ISO/IEC 1 5946 does not specify the implementation of the techniques it defines. Interoperability of products complying with ISO/IEC 1 5946 will not be guaranteed.
2 Normative reference(s)
The following referenced documents are indispensable for the application of this document. For dated references, only the edition cited applies. For undated references, the latest edition of the referenced document (including any amendments) applies.
ISO/IEC 1 5946-1 , Information technology — Security techniques — Cryptographic techniques based on elliptic curves — Part 1: General
3 Terms and definitions
For the purposes of this document, the following terms and definitions apply.
3.1
definition field of an elliptic curve
field that includes all the coefficients of the equation describing an elliptic curve
3.2
elliptic curve
cubic curve without a singular point
NOTE 1 A definition of a cubic curve is given in [29]
NOTE2 The set of points of E under a certain addition law forms an abelian group. In this part of lSO/EC 15946, weonly deal with finite fields F as the definition field. When we describe the definition field F of an elliptic curve E explicity, wedenote the curve as E/F.
NOTE 3 A detailed definition of an elliptic curve is given in Clause 4.[ISO/IEC 15946-1:2008]
3.3
finite field
field containing a finite number of elementsNOTE 1A definition of field is given in [29].
NOTE2 For any positive integer m and a prime p, there exists a finite field containing exactly pm elements. This field isunique up to isomorphism and is denoted by F(pm), where p is called the characteristic of F(pm).
[ISO/IEC 15946-1:2008]
3.4
hash-function
function which maps strings of bits to fixed-length strings of bits, satisfying the following two properties:
– for a given output, it is computationally infeasible to find an input which maps to this output;
– for a given input, it is computationally infeasible to find a second input which maps to the same output.[ISO/IEC10118-1]
NOTE 1 Computational feasibility depends on the specific security requirements and environment.
NOTE2 For the purposes of this document, the recommended hash-functions are those defined in lSOIEC 10118-2and lSO/IEC 10118-3.
3.5
nearly prime number
positive integer n = m-r, where m is a large prime number and r is a small smooth integer
NOTE The meaning of the terms large and small prime numbers is dependent on the application, and is based onbounds determined by the designer.
3.6
order of an elliptic curve E(F)
number of points on an elliptic curve E defined over a finite field F